http:// tangencias-potencia.blogspot.com/
http://inversas-de-figuras.blogspot.com/
1- Una circunferencia se transforma en una recta según se incrementa su radio: una recta es una circunferencia de radio infinito.

-----------------------------------------------------------------------------------------------------
2- Una inversión es una simetría axial en la que el eje se transforma en una circunferencia. La simetría axial divide el plano en dos semiplanos y los elementos de uno son inversos del otro; en la inversión hay dos superficies, la comprendida dentro de la circunferencia y la exterior a la misma.
Para calcular el inverso de un punto interno A se hace un segmento OA y se prolonga hasta que corte a la tangente por T, punto de intersección de la circunferencia y la perpendicular a OA por A.
A y A’ son inversos y siempre están alineados con O, que es el centro de inversión. Los puntos inversos de la circunferencia roja son dobles (inversos de sí mismos) por lo que se llama de autoinversión.

-----------------------------------------------------------------------------------------------------
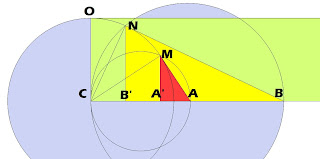
3- Si por B hacemos la tangente a la circunferencia y en el punto N de tangencia la perpendicular a CA tenemos el inverso de B que es B’.
Análogamente el de A es A’ y el inverso del infinito en la dirección CB es el centro C ya que la tangente a la circunferencia por O corta a la línea CB en el infinito.
El inverso del centro de inversión C está por tanto en el infinito.
-----------------------------------------------------------------------------------------------------
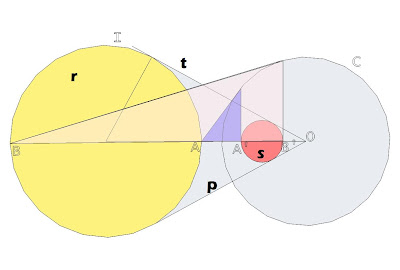
4- Para calcular la inversa de una circunferencia amarilla r desde el centro de inversión O y tomando como circunferencia de puntos dobles o de autoinversión C, unimos los dos centros de C y r. Desde la intersección A, B, de r con la línea que une los centros hacemos los inversos de A y B, que son A’ y B’. La nueva circunferencia inversa de I es la roja que tiene por diámetro el segmento A’-B’.
Como la inversión conserva las tangentes, si trazamos dos rectas t, p tangentes a una circunferencia cualquiera (p. ej., r) desde O, se tiene que las rectas t, p también son tangentes a la circunferencia s, por ser inversas una de la otra.
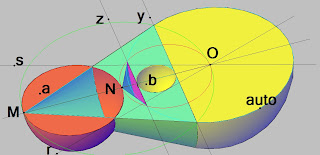
6- Existe una interpretación espacial para la inversión y sirve para hacer ejercicios de esferas tangentes cuyos centros estén en un mismo plano.
La inversión espacial de centro O y esfera de autoinversión auto transforma la esfera b en a de forma que desde O existe un cono tangente a las dos esferas y se tiene que si desde los vértices M, N, (puntos de la esfera a diametralmente opuestos incidentes en la línea de centros de las esferas y del centro de inversión) se hacen 2 conos respectivamente tangentes a la esfera auto, sus bases son tangentes a la esfera b.
-----------------------------------------------------------------------------------------------------
7- Aquí tenemos casos posibles de figuras inversas con la circunferencia de autoinversión (rellena de color gris): del 1 al 4 observamos la inversa de una recta que es una circunferencia roja que siempre pasa por el centro de inversión excepto si la recta pasa por éste, cuya inversa es entonces la misma recta pero no sus puntos.
Del 5 al 10 observamos la inversa de una circunferencia roja que se transforma en azul. En el caso 11 se transforma en sí misma y en el 9 la azul va hasta el infinito pues su inversa roja pasa por el centro de inversión.

-----------------------------------------------------------------------------------------------------
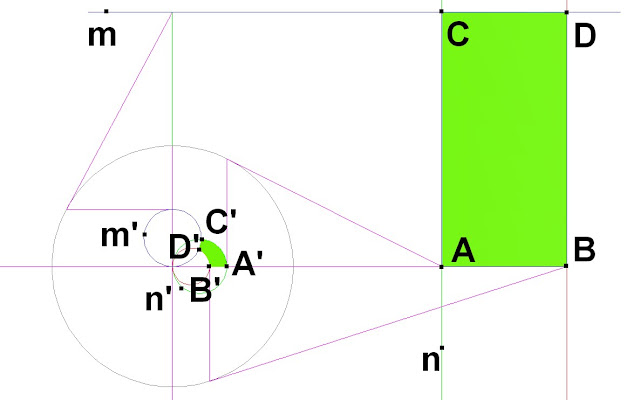
8- Por regla general una recta se transforma en circunferencia por inversión. En la figura un rectángulo ABCD tiene por inverso a un cuadrilátero A’B’C’D’ cuyos lados son curvos, excepto el lado AB (por pasar por el centro de inversión) que se transforma en la misma recta pero con otros puntos inversos como se ve en la figura.
-----------------------------------------------------------------------------------------------------
9- Una forma de intuir rápidamente las inversas de figuras es pensar en un triángulo rectángulo cuyos extremos de la hipotenusa inciden en la circunferencia inversa y la circunferencia autoinversa. En el momento en que los puntos de la recta m, inversa de m’, salen del interior de la circunferencia autoinversa los puntos se intercambian, la hipotenusa la forman los puntos de la circunferencia autoinversa y los de la recta m.

-----------------------------------------------------------------------------------------------------
10 a- Según el teorema del cateto, demostrado en la p.:http://figuras-equivalentes.blogspot.com/, el cuadrado rosa y el rectángulo amarillo tienen el mismo área, o lo que es lo mismo, el cateto OA del triángulo verde es a su hipotenusa OB, como el cateto OB del triángulo verde más azul es a su hipotenusa OA’, ya que ambos son proporcionales:
OA/OB = OB/OA’, por tanto OA. OA’= OB. OB = k.
Como vemos A A’ son inversos respecto al centro O y a la circunferencia de autoinversión (de color negra), por lo que en toda inversión se cumple: OA. OA’= OB. OB = k.

----------------------------------------------------------------------------------------------------
10 b-
En el número 1 a la izquierda tenemos el teorema del cateto: de la proporcionalidad entre los triángulos se desprende que el área del rectángulo verde es igual al área del cuadrado violeta.
1- Una circunferencia se transforma en una recta según se incrementa su radio: una recta es una circunferencia de radio infinito.

-----------------------------------------------------------------------------------------------------
2- Una inversión es una simetría axial en la que el eje se transforma en una circunferencia. La simetría axial divide el plano en dos semiplanos y los elementos de uno son inversos del otro; en la inversión hay dos superficies, la comprendida dentro de la circunferencia y la exterior a la misma.
Para calcular el inverso de un punto interno A se hace un segmento OA y se prolonga hasta que corte a la tangente por T, punto de intersección de la circunferencia y la perpendicular a OA por A.
A y A’ son inversos y siempre están alineados con O, que es el centro de inversión. Los puntos inversos de la circunferencia roja son dobles (inversos de sí mismos) por lo que se llama de autoinversión.

-----------------------------------------------------------------------------------------------------
3- Si por B hacemos la tangente a la circunferencia y en el punto N de tangencia la perpendicular a CA tenemos el inverso de B que es B’.
Análogamente el de A es A’ y el inverso del infinito en la dirección CB es el centro C ya que la tangente a la circunferencia por O corta a la línea CB en el infinito.
El inverso del centro de inversión C está por tanto en el infinito.

-----------------------------------------------------------------------------------------------------
4- Para calcular la inversa de una circunferencia amarilla r desde el centro de inversión O y tomando como circunferencia de puntos dobles o de autoinversión C, unimos los dos centros de C y r. Desde la intersección A, B, de r con la línea que une los centros hacemos los inversos de A y B, que son A’ y B’. La nueva circunferencia inversa de I es la roja que tiene por diámetro el segmento A’-B’.
Como la inversión conserva las tangentes, si trazamos dos rectas t, p tangentes a una circunferencia cualquiera (p. ej., r) desde O, se tiene que las rectas t, p también son tangentes a la circunferencia s, por ser inversas una de la otra.

--------------------------------------------------------------------------------------
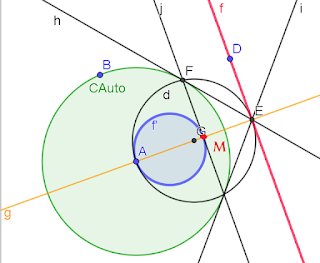
5- Calcular la circunferencia de autoinversión dada una recta f y una circunferencia f’ inversas, indistintamente.
1º- Se hace una recta g naranja que pase por el centro de la circunferencia azul y que sea perpendicular a la recta roja f
2º- Esa recta corta ambos elementos en los puntos A E
3º- Tomamos el Punto medio G del segmento AE
4º- Calculamos una circunferencia de centro G y radio AG, es la circunferencia negra llamada d
5 º- Por el punto de contacto M de la circunferencia azul y la recta naranja hacemos una perpendicular j, a la recta naranja (o paralela a la recta roja f, que es lo mismo)
6º- Esa recta j corta a la circunferencia d en el punto F
7º- La circunferencia que tiene por centro el punto A y el radio AF es la circunferencia de autoinversión, la solución.
-------------------------------------------------------------------------------------------
6- Existe una interpretación espacial para la inversión y sirve para hacer ejercicios de esferas tangentes cuyos centros estén en un mismo plano.
La inversión espacial de centro O y esfera de autoinversión auto transforma la esfera b en a de forma que desde O existe un cono tangente a las dos esferas y se tiene que si desde los vértices M, N, (puntos de la esfera a diametralmente opuestos incidentes en la línea de centros de las esferas y del centro de inversión) se hacen 2 conos respectivamente tangentes a la esfera auto, sus bases son tangentes a la esfera b.

-----------------------------------------------------------------------------------------------------
7- Aquí tenemos casos posibles de figuras inversas con la circunferencia de autoinversión (rellena de color gris): del 1 al 4 observamos la inversa de una recta que es una circunferencia roja que siempre pasa por el centro de inversión excepto si la recta pasa por éste, cuya inversa es entonces la misma recta pero no sus puntos.
Del 5 al 10 observamos la inversa de una circunferencia roja que se transforma en azul. En el caso 11 se transforma en sí misma y en el 9 la azul va hasta el infinito pues su inversa roja pasa por el centro de inversión.

-----------------------------------------------------------------------------------------------------
8- Por regla general una recta se transforma en circunferencia por inversión. En la figura un rectángulo ABCD tiene por inverso a un cuadrilátero A’B’C’D’ cuyos lados son curvos, excepto el lado AB (por pasar por el centro de inversión) que se transforma en la misma recta pero con otros puntos inversos como se ve en la figura.

-----------------------------------------------------------------------------------------------------
9- Una forma de intuir rápidamente las inversas de figuras es pensar en un triángulo rectángulo cuyos extremos de la hipotenusa inciden en la circunferencia inversa y la circunferencia autoinversa. En el momento en que los puntos de la recta m, inversa de m’, salen del interior de la circunferencia autoinversa los puntos se intercambian, la hipotenusa la forman los puntos de la circunferencia autoinversa y los de la recta m.

-----------------------------------------------------------------------------------------------------
10 a- Según el teorema del cateto, demostrado en la p.:http://figuras-equivalentes.blogspot.com/, el cuadrado rosa y el rectángulo amarillo tienen el mismo área, o lo que es lo mismo, el cateto OA del triángulo verde es a su hipotenusa OB, como el cateto OB del triángulo verde más azul es a su hipotenusa OA’, ya que ambos son proporcionales:
OA/OB = OB/OA’, por tanto OA. OA’= OB. OB = k.
Como vemos A A’ son inversos respecto al centro O y a la circunferencia de autoinversión (de color negra), por lo que en toda inversión se cumple: OA. OA’= OB. OB = k.

----------------------------------------------------------------------------------------------------
10 b-
En el número 1 a la izquierda tenemos el teorema del cateto: de la proporcionalidad entre los triángulos se desprende que el área del rectángulo verde es igual al área del cuadrado violeta.
Los puntos rojos CC' son inversos respecto al centro A -en color amarillo- de inversión, sabiendo que la circunferencia azul es la de autoinversión.
En el número 2 tenemos que si varios puntos, p. ej. PLMQ, están en una circunferencia, sus inversos también están en la misma circunferencia que es inversa de sí misma (circunferencia doble) mientras que en la parte inferior tenemos dos circunferencias verdes que son inversas y por tanto son homotéticas respecto al centro de inversión J, en color amarillo.

-----------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------
-------------------------------------------------------------
13- Cualquier circunferencia que contenga dos puntos inversos es ortogonal a la circunferencia de autoinversión.
Ello es debido a que las circunferencias son inversas de sí mismas (como la d) y por tanto desde el centro de inversión se pueden trazar las líneas que pasan por los puntos de intersección (E) con la circunferencia y obtener así las tangentes (h) a la misma desde el centro.
Los radios h i de ambas circunferencias por el punto de intersección E siempre serán ortogonales entre sí, pase por donde pase la circunferencia de centro D (sabemos que el centro D debe estar en la mediatriz de los 2 puntos inversos C-C').

-----------------------------------------------------------------------------------------------
11- Inversión negativa
Figura número 1:
Podemos ver una inversión positiva, la circunferencia de autoinversión de centro I, y radio iJ,
en color gris, transforma el triángulo rosa exterior en el triángulo verde. Ambas figuras son
inversas respecto al centro I.
en color gris, transforma el triángulo rosa exterior en el triángulo verde. Ambas figuras son
inversas respecto al centro I.
IH.IH’= k
Si ahora construimos la figura simétrica central del triángulo verde obtenemos el triángulo azul.
Figura número 2:
Ahora podemos decir que el triángulo rosa se transforma mediante una inversión negativa en
el triángulo azul ya que IH.IH’’= - k,
el triángulo azul ya que IH.IH’’= - k,
Y como tenemos que H no es coincidente con H’’ no es un punto inverso de sí mismo y por lo
tanto no tiene puntos dobles y en consecuencia tampoco tiene circunferencia de autoinversión.
tanto no tiene puntos dobles y en consecuencia tampoco tiene circunferencia de autoinversión.
Si queremos hacer ejercicios con inversión negativa podemos simplificar si combinamos
la inversión positiva con la simetría central.
la inversión positiva con la simetría central.
-------------------------------------------------------------------------------------
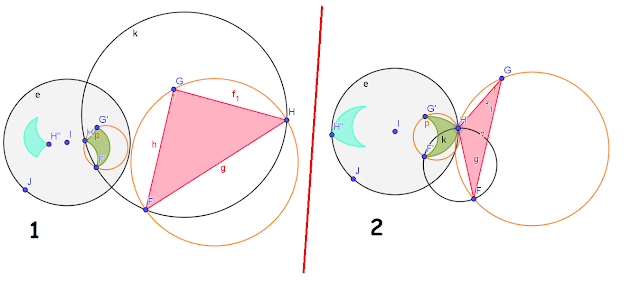
12- El centro de
una circunferencia de inversión respecto de la cual un triángulo es autopolar,
es el ortocentro de dicho triángulo
Dada una circunferencia de
autoinversión c y un cuadrilátero inscrito en color azul, al prolongar sus
lados tenemos los puntos FG, al hacer sus diagonales tenemos el punto H.
F, G, H determina un
triángulo autopolar ya que desde esos tres puntos se pueden trazar las 3
tangentes a la circunferencia que coinciden con la intersección de los lados
del triángulo con la circunferencia, pues realmente los lados del
triángulo son las polares respecto a cada vértice opuesto del triángulo.
Si
construimos las alturas del triángulo obtenemos el ortocentro A que
coincide con el centro de inversión, ello es debido a que las transformadas de
los tres lados del triángulo son tres circunferencias que pasan por el centro
de inversión y cada una de las alturas del triángulo que determinan en su
intersección el ortocentro son en realidad rectas perpendiculares a cada uno de
los lados desde los tres vértices del triángulo, esas tres alturas son inversas
de sí mismas ya que son perpendiculares a los lados del triángulo y por tanto
pasan por el centro de inversión.
-------------------------------------------------------------
13- Cualquier circunferencia que contenga dos puntos inversos es ortogonal a la circunferencia de autoinversión.
Ello es debido a que las circunferencias son inversas de sí mismas (como la d) y por tanto desde el centro de inversión se pueden trazar las líneas que pasan por los puntos de intersección (E) con la circunferencia y obtener así las tangentes (h) a la misma desde el centro.
Los radios h i de ambas circunferencias por el punto de intersección E siempre serán ortogonales entre sí, pase por donde pase la circunferencia de centro D (sabemos que el centro D debe estar en la mediatriz de los 2 puntos inversos C-C').


No hay comentarios:
Publicar un comentario